IMPORTANT DATES

 

 

St Agatha Science/Math FAIR
Project Schedule
2006 - 2007 


These dates are deadlines; try to get ahead of schedule in case a complication arises at some point; one usually does.
                       
October   2                             Start looking  for a topic
October   16                           Have topic and clearly state problem. Start working on form #1
November 15                         Last date for final proposal and any changes to your topic.
November 20 – 21                  Form #1
December 1                            Form #2
December 18                          Form #3
January 3 – January 10        Conference with Teacher
January 22                             Project Data is brought to class
January 24 – February 8      Oral presentation
February 15                           Logbook and research paper is submitted
March 5                                  Final class presentation
March 21                                Judging of project
 March 22                               Project Open house

   

Data Collection for Experimentation to be used as a guide

 

Designing a Table

Every table must have:

 

Working with Frequencies

Frequency Table
 Many times we count how many of something or how often something occurs. This usually means that the data will display in a frequency table. The example below is for an experiment in which the number of colds per year for a randomly sampled group was tallied.
 
 

HOW MANY COLDS A YEAR DO PEOPLE HAVE?

 

# of Colds
per Year

# of People

0

3

1

5

2

8

3

5

4

4

5

3

6

1



  top of page

 

Parts of a Graph

A graph is simply a picture of your data.  It tells a story, the story that the data should be telling us.  Someone should be able to look at your graph and, with no other information, be able to describe what you have learned from your project data.
Every graph must have:

Caution: If making graphs by computer, be careful to not make the graph so elaborate that it is difficult to read.  For example, 3-D computer graphs are colorful and visually appealing, but they are very difficult to read.  A simple but correct graph is always the best.

 

 

 

 

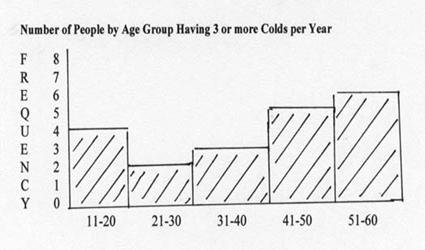
Histogram
  The histogram is like a bar graph with intervals. Sometimes we can get a more accurate picture of the data if we group data. In the example below we had many different ages, way too many to make a bar for each. By grouping the ages to 10 year intervals, it is much easier to see the change in frequency as age increases.



 

 

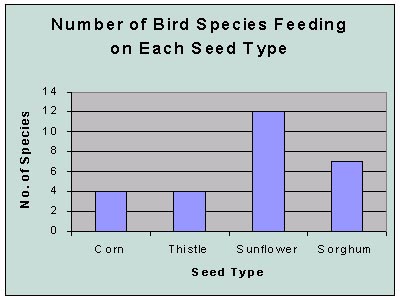
Bar Graph

We use a bar graph when we want to compare 2 - 4 groups.

Example: 
 


 top of page

Working with Percentages

 

Calculating Percentages

A percentage is a part of the whole. To calculate:

Percentage = Part/whole x 100 (number/total x 100)

Example: 12 students of a class of 25 are male
Percentage of males = 12/25 x 100 = 48%


Displaying Data in a Percent Table

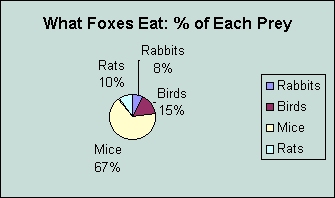
Example:

% of Animals Eaten by a Fox

Prey

Number Eaten

Percentage of Diet

Rabbits 

3 

7.5% 

Birds 

6 

15% 

Mice 

27

67.5% 

Rats 

4

10% 

 

 

 

Total

40 

100%

 

 

 

Making a Circle Graph (Pie Chart)

Steps to Making a Circle Chart:

1.  Calculating the Angles for Each "Pie Slice": The difficult part of making a circle chart is to convert each percentage of the whole to the degrees of angle that the "pie slice" will be of the circle. To do this, you multiply the percentage times 360o.

Example: (Using the data table above) 15% rabbits
                    Step 1: Convert percent to decimal 15% divided by 100 = 0.15
                    Step 2: Find degrees of angle of "pie slice" 0.15 x 360o = 54o
                    Step 3: Repeat for all percentages.
                    Step 4: Check accuracy of math by seeing if all angles add to 360o.

2.  Constructing the Circle Graph
Step 1: Draw a circle, and mark the center.
Step 2: Draw a radius.
Step 3: Use protractor to mark the angle for the first "pie slice".
Step 4: Repeat for each angle.
Step 5: Label each pie slice with identification and percentage.
Step 6: Include title.

Example:

  top of page

 

Measures of Central Tendency

Mean - average

    To calculate:
    1. Sum all data.
    2. Divide by the number of data points.
    3. Round off to one decimal place more than what each number is.

    Example:  1, 8, 3, 7, 2, 4, 6, 5           Sum = 36        # of data points = 8
                    Mean   =   36/8  =  4.5

Median - middle number

    To calculate:
    1. Arrange the numbers in order, and count down to the middle number.
    2. If there are an even number of data points, it will fall between 2 data points; average the two to get the median.

Mode - most common number

Example:  Pendulum frequencies -   25,25,24,25,25,23,25,25,25
                "25" is logically the "correct" reading since it appears most of the time.  Report the mode as 25.

Which Do I Use?

Mean - This is OK to use if data are evenly distributed. 
Median - This is better to use if you have outliers (numbers that are much higher or lower than the other numbers) because the outliers would significantly raise or lower the mean.  Use this number if you are doing a Box and Whisker Plot.
Mode - This is best to use if one number seems to be easily the most commonly appearing number; this would lead to the conclusion that it is the "correct number".

  top of page

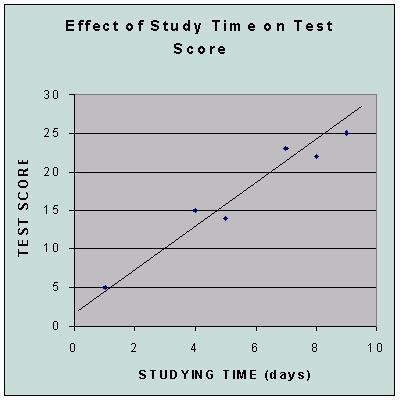
Comparing 2 Variables

 

Scatter Plot 

EXAMPLE:

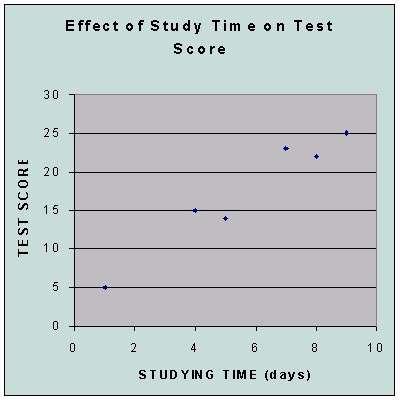
Line of Best Fit
The points in the scatter plot above look like they loosely form a line.  We can draw a line which roughly intersects these points.  We can then use a value (correlation) to find how close the points are to the line and find a formula for the line. 

 

 top of page